Probability and Base Rate Neglect

Continuing the theme of calculating probability being difficult…

Here is Bayes’ Theorem, which provides an objective measure of the probability of Event A occurring given that Event B occurs:

Where:

$P(B|A)$ is the probability of Event B given that Event A occurs

$P(A)$ is the probability of event A occurring

$P(B)$ is the probability of event B occurring – which, to further complicate things, is calculated by adding together the following:

$P(A) \times P(B|A)$ , which is the probability of A occurring multiplied by the probability of B occurring given that A occurs.

$P(\sim{A}) \times P(B|\sim{A})$ , which is the probability of A not occurring multiplied by the probability of B occurring given that A does not occur.

This is a common reaction when first encountering Bayes’ Theorem…

…so let’s look at an example:

Question 8

What is the probability that a woman who tests positive for breast cancer actually has breast cancer? To pin this question down, let us consider a population in which 1% of women have breast cancer, and a mammography test which has a 90% chance of returning a correct result. That is, if a woman has cancer then there is a 90% chance the test will be positive, and if a woman does not have cancer then there is a 90% chance the test will be negative. Suppose a particular woman tests positive; what is the probability that she has breast cancer?

Question

Was your answer based on an estimate or a calculation? Where do you think responses typically fall relative to the correct answer? Let’s have a look at how people have responded:

Bayes’ Theorem can be applied to give the correct answer to this problem. However, because this formula is so complicated, people tend to ignore or neglect the base rate (i.e., the prior probability of having breast cancer) in order to simplify the required calculations. Many people will say 90%, with an average of between 50% and 60%. The correct answer is slightly above 8%.

The example comes from the UK Breast Cancer Screening Program. One way to make the problem easier is to think about it in terms of concrete numbers, as shown in the diagram below:

In a group of 1000 women: 10 women (or 1%) have breast cancer, and 990 women (or 99%) do not have breast cancer. Continuing on, the 10 women with breast cancer split into 9 women (or 90%) who correctly test positive, and 1 woman (or 10%) who incorrectly test negative. The 990 women without breast cancer split into 99 women (or 10%) who incorrectly test positive, and 891 women (or 90%) who correctly test negative. From the bottom row we see that of the women who test positive, 9 have breast cancer and 99 do not have breast cancer. Therefore, the probability that a woman who tests positive for breast cancer actually has breast cancer is 9 in 108, which is roughly an 8% chance.

If we take Event A to be “has breast cancer” and Event B to “positive test result”, we can frame this in terms of Bayes Theorem:

$P(A) = 0.01$ (probability that a woman has breast cancer) – this is the base rate given that is given to you.

$P(\sim A) = 0.99$ (probability that a woman doesn’t have breast cancer) – this is the probability of A subtracted from 1.

$P(B|A) = 0.9$ (probability that a woman tests positive, given that she has breast cancer) – this is the hit rate of the test for women with breast cancer.

$P(B|\sim A) = 0.1$ (probability that a woman tests positive, given that she does not have breast cancer) – the is the false alarm rate for women who do not have breast cancer.

With these values, we want to calculate P(A|B), the probability that a woman has breast cancer if she tests positive.

$P(A|B) &= P(A) \times P(B|A) / [P(B|A) \times P(A) + P(B|\sim A) \times P(\sim A)] \\ &= 0.01 \times 0.9 / [0.9 \times 0.01 + 0.1 \times 0.99] \\ &= 0.009 / 0.108 \\ &= 0.083$

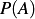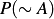If one was to neglect the base rate of occurrence of breast cancer (i.e., disregard $P(A)$ and $P(\sim A)$ ), then the calculation would be:

$P(A|B) &= P(B|A) / [P(B|A) + P(B|\sim A)] \\ &= 0.9 / (0.9 + 0.1) \\ &= 0.9$

This is the mathematical underpinning for how base rate neglect can lead to a gross overestimation of the implication of a positive result on the breast cancer screening test. Thomas Bayes would certainly have had something to say about that!

Thomas Bayes